Algoritmos de búsqueda por comparación

Análisis de algoritmos

Julia

Algoritmos de búsqueda

Búsqueda binaria

Búsqueda acotada

Análisis de algoritmos de búsqueda adaptativa en Julia, comparando eficiencia entre métodos binarios, secuenciales y SkipLists.

Autor/a

Santiago Botero Sierra

Fecha de publicación

1 de abril de 2025

Fecha de modificación

3 de junio de 2025

Ver el código

using Dates, DataFrames, JSON, MarkdownTables, Random, StatsPlots
rng = Xoshiro(20250331)

Xoshiro(0xb6218ccaee99c301, 0xc600d4c1d7a2a0ea, 0x84b975df6153e011, 0x1dd4e5c247a2ef30, 0x7095a0bd51999064)

1 Introducción

Téllez Avila (2025, cap. 5) discute algoritmos adaptables de búsqueda en arreglos organizados. En el modelo de comparación, estos algoritmos buscan identificar la posición de inserción, $p$, en la que debe acomodarse un valor $x$ para que el arreglo $A = (a_1, \dots, a_n), \, a_1 \leq \dots \leq a_n$ se mantenga ordenado después de la inserción de $x$.

En la Sección 2 se presentan e implementan en Julia los algoritmos analizados, tanto para el caso base (la búsqueda binaria), cuyo costo depende del tamaño del arreglo, como para los algoritmos adaptables. Como se observa en dicha sección, la particularidad de estos últimos es que su costo de ejecución depende de $p$ y no del tamaño del arreglo.

A continuación, en la Sección 3 se implementan diversos experimentos para probar cada algoritmo en cuanto al tiempo de ejecución y el número de operaciones de comparación requeridas. Al respecto, se observa que en los experimentos realizados no se observa una tendencia clara en los datos que permita identificar si se satisface la expectativa de que el tiempo de ejecución y el número de operaciones de los algoritmos analizados dependen de $p$.

Por lo tanto, en la Sección 4 se concluye que se requiere mayor investigación para determinar la causa del comportamiento inesperado.

2 Algoritmos de búsqueda

En esta sección se analizan diversos algoritmos de búsqueda descritos en Téllez Avila (2025, cap. 5), así como una implementación propia de un algoritmo de búsqueda sobre SkipLists. Para cada uno, se explica cuál es el costo del problema y se describe una función en Julia para su implementación.

2.1 Búsqueda binaria acotada

La búsqueda binaria en el subarreglo $A[i:f]$ consiste en verificar si $x$ se encuentra antes o después del punto medio, $m = \lfloor \frac{i + f}{2} \rfloor$, para lo cual se debe comparar $x$ con $a_m$, actualizar $i$ o $f$ para continuar la búsqueda en un arreglo de la mitad del tamaño e iterar hasta llegar al caso base, en donde $i \geq f$. Cuando se llega a ese punto, entonces únicamente hay que comparar $x$ con el valor de $a_i$ correspondiente y seleccionar $p$ como $i$ o $i + 1$, dependiendo del resultado obtenido. Esta implementación obtiene un costo de búsqueda de $O(\log_2 n)$ (Téllez Avila 2025, sec. 5.1.1).

Este algoritmo fue implementado en Julia mediante la función busqueda_binaria(), en la que se adicionó un argumento opcional para contabilizar el número de veces que se calcula el punto medio, que corresponde al costo del problema.

Ver el código

function busqueda_binaria(
    A::Vector{T}, 
    x::T, 
    c::Union{Nothing, Int64} = nothing,
    inicio::Int64 = 1, 
    final::Int64 = length(A) ) where {T}
    while inicio < final
        medio = (inicio + final) ÷ 2
        if x <= A[medio]
            final = medio
        else
            inicio = medio + 1
        end
        
        if c isa Int64
            c += 1
        end
    end
    p = x <= A[inicio] ? inicio : inicio + 1
    return p, c
end

busqueda_binaria (generic function with 4 methods)

De acuerdo con Téllez Avila (2025, sec. 5.2), cuando $n \to \infty$ o la relación $\frac{p}{n} \to 0$, es más útil definir un rango que pueda contener la respuesta antes de aplicar la búsqueda binaria. Esto se puede implementar mediante una familia de algoritmos $B_k$, cuyos primeros miembros se explican e implementan en las siguientes subsecciones. También se explica un algoritmo basado en la estructura SkipLists que tiene esta misma inspiración.

Con base en esta observación, el único algoritmo de búsqueda que depende del tamaño del arreglo, $n$, que se analiza en este documento es el implementado mediante busqueda_binaria(). En las siguientes subsecciones, se presentan algoritmos adaptativos que dependen de $p$.

2.2 Búsqueda secuencial $B_0$

Sea $F_0(n) = 1, 2, \dots, n, n + 1$ una secuencia de puntos en los que se harán comparaciones entre $x$ y $a_{F_0(n)}$. Es decir, este algoritmo implementa una búsqueda exhaustiva al comparar $x$ con cada valor del arreglo $A$, por lo que no requiere una búsqueda binaria y su costo de búsqueda corresponde a todas las comparaciones que se deben hacer hasta llegar a la posición de inserción $C_0(p) = p + 1$ (Téllez Avila 2025, sec. 5.2.1).

Para implementar el algoritmo, se debe iniciar la búsqueda en el primer elemento de A y continuarla hasta que se encuentre el elemento de $A$ que sea mayor que $x$ o se recorra todo el arreglo, entonces la posición de inserción de $x$ será la posición de dicho elemento (Téllez Avila 2025, sec. 5.1.1).

Este algoritmo se implementó en Julia mediante la función busqueda_b0(), en la que se adicionó un argumento opcional para contabilizar el número de veces que se realizan comparaciones, que corresponde al costo del problema.

Ver el código

function busqueda_b0(
    A1::Vector{T},
    x::T,
    c::Union{Nothing, Int64} = nothing,
    inicio::Int64 = 1) where {T}
    p = 1
    A = A1[inicio:end]
    n = length(A)
    while p <= n && x > A[p]
        p += 1
        if c isa Int64
            c += 1
        end
    end
    return p, c
end

busqueda_b0 (generic function with 3 methods)

2.3 Búsqueda secuencial $B_1$

Sea $F_1(n) = 2^1, 2^2, \dots, 2^{\lfloor \log_2 n \rfloor + 1}$ una secuencia de puntos en los que se harán comparaciones entre $x$ y $a_{F_1(n)}$, que servirán para determinar el rango en el que se realizará la búsqueda binaria $A[2^{\lfloor \log_2 p \rfloor + 1}:2^{\lfloor \log_2 (p + 1) \rfloor + 1}]$; entonces, dependiendo de la posición $p$, el número de comparaciones que se deben realizar para determinar este rango está determinado por $\lfloor \log_2 p + 1 \rfloor + 1$. Una vez determinado, el costo de la búsqueda en dicho rango está limitado por $O(\log_2 n^\prime)$ donde $n^\prime$ es el tamaño del arreglo en el que se realiza la búsqueda binaria. Por lo tanto, el costo total de la búsqueda implementada es $C_1(p) < 2 \log_2 p + O(1)$ (Téllez Avila 2025, sec. 5.2.2).

Este algoritmo se implementó en Julia mediante la función busqueda_b1(), en la que se adicionó un argumento opcional para contabilizar el número de veces que se realizan comparaciones, que corresponde al costo del problema.

Ver el código

function busqueda_b1(
    A1::Vector{T}, 
    x::T,
    c::Union{Nothing, Int64} = nothing,
    inicio::Int64 = 1) where {T}
    A = A1[inicio:end]
    n = length(A)
    p = 0

    # Determinar el rango
    # Duplicar la posición de búsqueda e ir actualizando la posición de inicio
    iteracion = 1
    while iteracion + 1 <= n && A[iteracion + 1] < x
        p = iteracion
        iteracion *= 2

        if c isa Int64
            c += 1
        end
    end

    # Realizar la búsqueda dentro del rango
    p, c = busqueda_binaria(A, x, c, p + 1, min(n, iteracion + 1))
    
    return p, c
end

busqueda_b1 (generic function with 3 methods)

2.4 Búsqueda secuencial $B_2$

Sea $F_2(n) = 2^{2^1}, 2^{2^2}, \dots, 2^{2^{\lfloor \log_2 \lfloor \log_2 (p + 1) + 1 \rfloor + 1}}$ una secuencia de puntos en los que se harán comparaciones entre $x$ y $a_{F_2(n)}$, que servirán para determinar el rango en el que se realizará la búsqueda de información $A[2^{2 \lfloor \log_2 \lfloor \log_2 p \rfloor + 1 \rfloor + 1}:2^{2 \lfloor \log_2 \lfloor \log_2 (p + 1) \rfloor + 1 \rfloor + 1}]$; entonces, dependiendo de la posición $p$, el número de comparaciones que se deben realizar para determinar este rango está determinado por $\lfloor \log_2 \lfloor \log_2 (p + 1) \rfloor + 1 \rfloor + 1$. Una vez determinado este rango, se puede aplicar la búsqueda $B_1$ sobre él. Por lo tanto, el costo total de la búsqueda implementada es $C_2(p) < \log_2 p + 2 \log_2 \log_2 p + O(1)$ (Téllez Avila 2025, sec. 5.2.2).

Este algoritmo se implementó en Julia mediante la función busqueda_b2(), en la que se adicionó un argumento opcional para contabilizar el número de veces que se realizan comparaciones, que corresponde al costo del problema.

Ver el código

function busqueda_b2(
    A1::Vector{T}, 
    x::T,
    c::Union{Nothing, Int64} = nothing,
    inicio::Int64 = 1 ) where {T}

    A = A1[inicio:end]
    n = length(A)
    p1 = 0

    # Determinar el rango
    # Duplicar la posición de búsqueda e ir actualizando la posición de inicio
    iteracion = 1
    valor = 2^(2^iteracion)
    while valor + 1 <= n && A[valor + 1] < x
        p1 = valor
        iteracion += 1
        valor = 2^(2^iteracion)

        if c isa Int64
            c += 1
        end
    end

    # Realizar la búsqueda dentro del rango
    p, c = busqueda_b1(A[(p1 + 1):min(valor, n)], x, c)
    
    return p + p1, c
end

busqueda_b2 (generic function with 3 methods)

2.5 Busqueda mediante SkipLists

Como se explicó en el post sobre algoritmos de ordenamiento, se puede implementar una “SkipList” en Julia mediante las estructuras mutables Nodo y Lista_Salto, como se muestra a continuación. A partir de estas estructuras, se pueden definir funciones para modificar la lista al insertar elementos en ella, inserta_skiplist!(), y utilizar el resultado obtenido para ordenar un arreglo, ordenar_skiplist().

Ver el código

# 1. Estructuras de datos
# Nodos
mutable struct Nodo{T}
    valor::T
    sucesores::Vector{ Union{Nodo{T}, Nothing} }
end

Nodo{T}(valor::T, nivel::Int64) where {T} = Nodo{T}(
    valor, 
    Vector{ Union{Nodo{T}, Nothing} }(nothing, nivel) )
Nodo(valor::T, nivel::Int64) where {T} = Nodo{T}(valor::T, nivel::Int64)

# Listas
mutable struct Lista_Salto{T}
    nivel_maximo::Int64
    cabeceras::Vector{ Union{Nodo{T}, Nothing} }
end

Lista_Salto{T}() where {T} = Lista_Salto(
    1, 
    Vector{ Union{Nodo{T}, Nothing}}(nothing, 1) )
Lista_Salto() = Lista_Salto{Float64}()

# 2. Función inserta_skiplist!()
function inserta_skiplist!(
    lista::Lista_Salto{T}, 
    valor::T, 
    c::Union{ Int64, Nothing } = nothing,
    rng = nothing) where {T}
    # Asignar aleatoriamente un nivel
    nivel = 1
    if rng isa Nothing
        while rand() <= 0.5
            nivel += 1
        end
    else
        while rand(rng) <= 0.5
            nivel += 1
        end
    end

    # Si la lista tiene menos niveles, adicionar los restantes
    if nivel > lista.nivel_maximo
        for k in (lista.nivel_maximo + 1):nivel
            push!(lista.cabeceras, nothing)
        end
        lista.nivel_maximo = nivel
    end

    # Nuevo nodo
    y = Nodo{T}(valor, nivel)
    
    # Actualizar los punteros desde el máximo nivel que estoy insertando
    for k in nivel:-1:1
        # Contabilizar el número de actualizaciones del puntero
        if c isa Int64
            c += 1            
        end

        x = lista.cabeceras[k]
        if x isa Nothing
            # Si el nivel k de la cabecera está vacío, entonces apunta
            # al nuevo nodo
            lista.cabeceras[k] = y
        elseif valor < x.valor
            # Si lo que se inserta es pequeño, entonces se actualiza desde
            # el principio
            lista.cabeceras[k] = y
            y.sucesores[k] = x
        else
            # Si no está vacío, buscamos hasta que el nivel de algún 
            # sucesor sea menor y quebramos los apuntadores
            z = x.sucesores[k]
            while !(z isa Nothing) && (valor > z.valor)
                x = z
                z = z.sucesores[k]
            end
            x.sucesores[k] = y
            y.sucesores[k] = z
        end
    end
    return c
end

# 3. Función ordenar_skiplist()
function ordenar_skiplist(
    a::Vector, 
    c::Union{ Int64, Nothing } = nothing, 
    rng = nothing)
    listado = Lista_Salto{eltype(a)}()
    ordenar = Vector{eltype(a)}()
    for elemento in a
        c = inserta_skiplist!(listado, elemento, c, rng)
    end
    siguiente = listado.cabeceras[1]
    while !(siguiente isa Nothing)
        push!(ordenar, siguiente.valor)
        siguiente = siguiente.sucesores[1]
    end
    return c, ordenar, listado
end

ordenar_skiplist (generic function with 3 methods)

En adición a los elementos señalados, que ya habían sido analizados en ese post, se generó la función busqueda_skiplist(), que implementa un algoritmo adaptativo para buscar un valor $x$ en una SkipList. A diferencia de los algoritmos señalados en las subsecciones anteriores, este no entrega la posición en la cual se debe insertar el valor para conservar el orden del arreglo, pues ello no tiene sentido para una SkipList, sino que entrega la referencia del nodo que sería antecesor al que se construya a partir del valor que se desea insertar, de forma que los apuntadores después de insertar el nodo con este valor mantengan el ordenamiento de la lista. El procedimiento implementado se describe a continuación:

Se busca el valor al que apuntan las cabeceras de la lista en las posiciones $F(n) = 2^0, 2^1, \dots, 2^{\lfloor \log_2 n + 1 \rfloor}$.
Se identifica el nodo con el valor más grande en dicha lista, cuyo valor es inferior al valor buscado $x$. Es decir, se reduce la dimensionalidad del rango buscado al eliminar los primeros nodos más pequeños que el valor buscado.
Se realiza una búsqueda descendiendo de nivel, del nodo más grande en la lista que es inferior al valor buscado.

Se adicionó un parámetro opcional en esta función que contabiliza el número de comparaciones que realiza el algoritmo, que es proporcional a su costo de ejecución. Debido al primer inciso señalado, se espera que este costo sea proporcional al valor de $p$, no al tamaño completo de la SkipList.

Ver el código

function busqueda_skiplist(
    lista::Lista_Salto{T}, 
    valor::T, 
    c::Union{ Int64, Nothing } = nothing ) where {T}
    k = 1
    while k <= lista.nivel_maximo && lista.cabeceras[k].valor < valor
        k *= 2

        if c isa Int64
            c += 1
        end
    end
    k = min(k, lista.nivel_maximo)

    if lista.cabeceras[k].valor >= valor
        inferior = lista.cabeceras
    else
        inferior = lista.cabeceras[k]
        while k >= 1
            # Contabilizar el número de actualizaciones del puntero
            if c isa Int64
                c += 1            
            end
            
            siguiente = inferior.sucesores[k]
            if siguiente isa Nothing || siguiente.valor >= valor
                k -= 1
            else
                # Si no está vacío, buscamos hasta que el nivel de algún 
                # sucesor sea menor y quebramos los apuntadores
                inferior = siguiente
            end
        end
    end
    return inferior, c
end

busqueda_skiplist (generic function with 2 methods)

3 Experimentos

Como fue señalado en la sección anterior, se espera que el costo de ejecución de busqueda_binaria() sea proporcional al tamaño del arreglo, mientras que el de las demás funciones debería ser proporcional a $p$. En este sentido, en esta sección se realizan experimentos con diversos valores de $p$ para verificar si se satisface esta expectativa teórica en las funciones implementadas. En la Sección 3.1 se describen los datos utilizados y las consultas que fueron realizadas sobre ellos. En la Sección 3.2, se analizan los tiempos de ejecución y en la Sección 3.3 se contabiliza el número de operaciones. En ambos casos, se observa que se los resultados obtenidos no fueron los esperados.

3.1 Datos

Se generó el mismo diccionario denominado datos disponible en el el post sobre algoritmos de ordenamiento.

Ver el código

datos = Dict()
for numero in ["016", "032", "064", "128", "256", "512"]
    datos[parse(Int64, numero)] = JSON.parsefile(
        "../20250304-algoritmos_ordenamiento/listas-posteo-con-perturbaciones-p=$(numero).json" )
end
for numero in keys(datos)
    for asunto in keys(datos[numero])
        datos[numero][asunto] = convert(Vector{Int64}, datos[numero][asunto])
    end
    datos[numero] = convert(Dict{String, Vector{Int64}}, datos[numero])
end
datos = convert(Dict{Int64, Dict{String, Vector{Int64}}}, datos)

Como las funciones busqueda_binaria(), busqueda_b0(), busqueda_b1() y busqueda_b2() requieren como entrada un arreglo ordenado y la función busqueda_skiplist() requiere una SkipList, entonces se procesaron los arreglos desordenados originalmente disponibles en cada diccionario interior para convertirlos en uno de estos dos tipos de insumo. Para ello, cada uno de los arreglos originales se procesó mediante la función ordenar_skiplist() y se conservaron las respuestas del arreglo ordenado y la SkipList que se obtienen a partir de esta función; estos arreglos se registraron en los diccionarios denominados ordenado y skiplist, respectivamente.

Ver el código

ordenado = Dict{Int64, Dict{String, Vector{Int64}}}()
skiplist = Dict{Int64, Dict{String, Lista_Salto{Int64}}}()
for numero in keys(datos)
    ordenado[numero] = Dict{String, Vector{Int64}}()
    skiplist[numero] = Dict{String, Lista_Salto{Int64}}()
    for asunto in keys(datos[numero])
        _, x, y = ordenar_skiplist( datos[numero][asunto] )
        ordenado[numero][asunto] = x
        skiplist[numero][asunto] = y
    end
end

Asimismo, se obtuvieron números para consultar en los diferentes arreglos a partir de 4 archivos electrónicos, disponibles aquí.¹ Estos se registraron en un diccionario denominado consultas, cuyas claves son asociadas al archivo electrónico correspondiente y cuyos valores son los arreglos con los números de consulta que se realizarán.

Ver el código

consultas = Dict()
for numero in [1, 2, 3, 4]
    consultas[numero] = JSON.parsefile("consultas-$(numero)-listas-posteo.json")
end
for numero in keys(consultas)
    consultas[numero] = convert(Vector{Int64}, consultas[numero])
end
consultas = convert(Dict{Int64, Vector{Int64}}, consultas)

3.2 Tiempo de ejecución

Se observó que cada una de las claves en ordenado contienen vectores con la misma información. Por lo tanto, únicamente se realizarán consultas sobre los vectores disponibles en ordenado[16] y skiplist[16], en lugar de hacerlo para cada clave en dichos diccionarios. Para cada una de las consultas disponibles en los elementos de consultas, se iteró 100 veces sobre los arreglos señalados y se midió el tiempo total de ejecución de las funciones disponibles en la Sección 2. Cada una de las observaciones se registró en un DataFrame denominado labbusc, que contiene los siguientes campos:

funcion, que contiene una abreviatura asociada a la función de búsqueda utilizada.
num_consulta, que corresponde al número del archivo de consulta utilizado.
consulta, que corresponde al valor buscado en los vectores de ordenado[16] y skiplist[16].
tiempo, que corresponde al tiempo total utilizado para realizar las 100 iteraciones de la consulta

Ver el código

experimentos = [
    ("busqueda_binaria", "BB"), 
    ("busqueda_b0", "B0"), 
    ("busqueda_b1", "B1"),
    ("busqueda_b2", "B2"), 
    ("busqueda_skiplist", "BSK")]

labbusc_tiempo = DataFrame(
    funcion = Vector{String}(), 
    num_consulta = Vector{Int64}(), 
    consulta = Vector{Int64}(), 
    tiempo = Vector{Float64}()
    )
n_iter = 100

# Vamos a guardar el número de la consulta, el experimento y cuánto se demora realizándola, 
# independientemente de la lista de posteo (ya da igual porque están organizados)
for num_consulta in 1:4
    for consulta in consultas[num_consulta]
        for experimento in experimentos
            # Midamos el tiempo que se demora cada función en buscar cada 
            # consulta en todos los vectores de las listas de posteo
            f = Symbol(experimento[1])
            f = getfield(Main, f)
            x = now()
            for asunto in keys(ordenado[16])
                for i in 1:n_iter
                    if experimento[1] != "busqueda_skiplist"
                            f(ordenado[16][asunto], consulta)
                    else
                            f(skiplist[16][asunto], consulta)
                    end
                end
                push!(labbusc_tiempo, 
                      (experimento[2], num_consulta, consulta, 
                       Dates.value( Millisecond(now() - x) ) ) )
            end
        end
    end
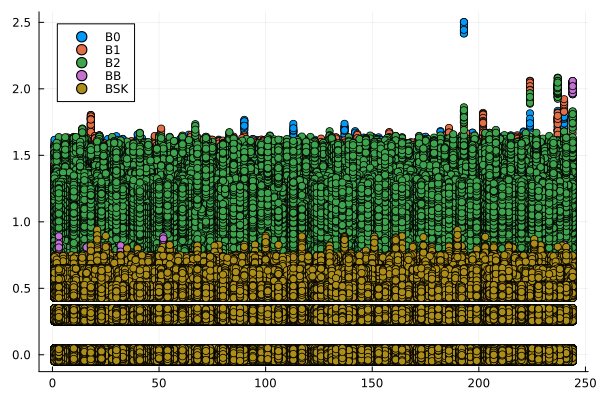
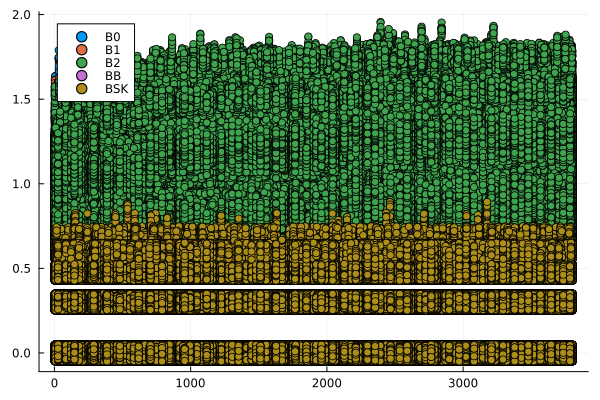
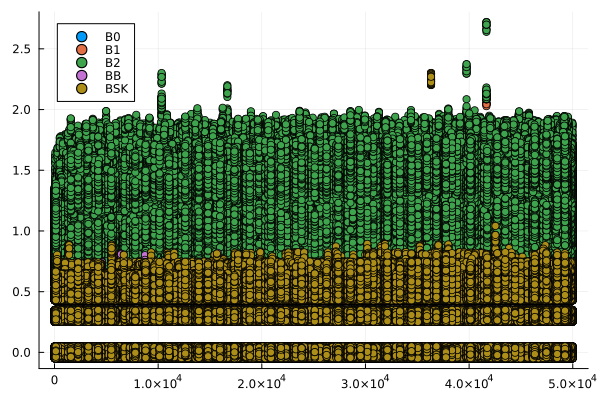
end

Con base en esta información se generaron gráficos de dispersión, para cada archivo de consultas, que muestran el logaritmo en base 10 del tiempo que toma cada función para ejecutar las consultas en los vectores ordenados como función del valor consultado $p$. Estas se muestran en la Figura 1.

Ver el código

jitter(n::Real, factor = 0.1) = n + (0.5 - rand()) * factor

labbusc_tiempo = filter(row -> !isnan(row.tiempo) && row.tiempo > 0, labbusc_tiempo)
for i in 1:4
    grafico = filter(row -> row.num_consulta == i, labbusc_tiempo)
    plot = @df grafico scatter(:consulta, jitter.(log10.(:tiempo)), group = :funcion) 
    savefig(plot, "busquedas_$(i)_tiempo.png")
end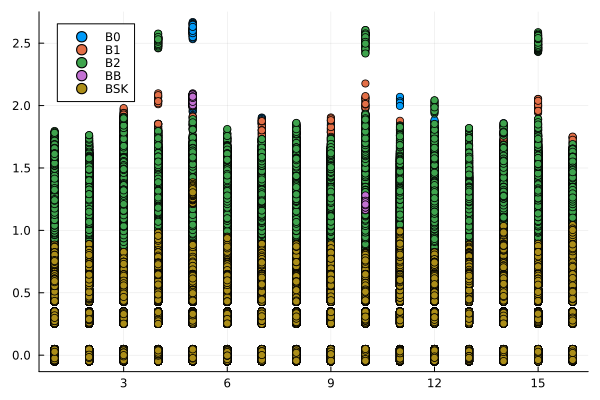

3.3 Contabilización del número de comparaciones

Homólogamente, se contabilizó el número de comparaciones que requirió cada algoritmo para realizar la búsqueda de cada valor. A diferencia del caso anterior, este experimento se realizó una única vez por experimento, pues el número de comparaciones es determinístico.

Ver el código

labbusc_cuenta = DataFrame(
    funcion = Vector{String}(), 
    num_consulta = Vector{Int64}(), 
    consulta = Vector{Int64}(), 
    contabilidad = Vector{Float64}()
    )

# Vamos a guardar el número de la consulta, el experimento y cuántas comparaciones hace, 
# independientemente de la lista de posteo (ya da igual porque están organizados)
for num_consulta in 1:4
    for consulta in consultas[num_consulta]
        for experimento in experimentos
            # Midamos el tiempo que se demora cada función en buscar cada 
            # consulta en todos los vectores de las listas de posteo
            f = Symbol(experimento[1])
            f = getfield(Main, f)
            x = now()
            for asunto in keys(ordenado[16])
                if experimento[1] != "busqueda_skiplist"
                    _, c = f(ordenado[16][asunto], consulta, 0)
                else
                    _, c = f(skiplist[16][asunto], consulta, 0)
                end
                push!(labbusc_cuenta, 
                      (experimento[2], num_consulta, consulta, c) )
            end
        end
    end
end

Con base en esta información se generaron gráficos de dispersión, para cada archivo de consultas, que muestran el número de comparaciones que requiere cada función para ejecutar las consultas en los vectores ordenados, como función del valor consultado $p$. Estas se muestran en la Figura 2.

Ver el código

labbusc_cuenta = filter(row -> !isnan(row.contabilidad) && row.contabilidad > 0, labbusc_cuenta)
for i in 1:4
    grafico = filter(row -> row.num_consulta == i, labbusc_cuenta)
    plot = @df grafico scatter(:consulta, jitter.(:contabilidad), group = :funcion) 
    savefig(plot, "busquedas_$(i)_cuenta.png")
end

4 Conclusión

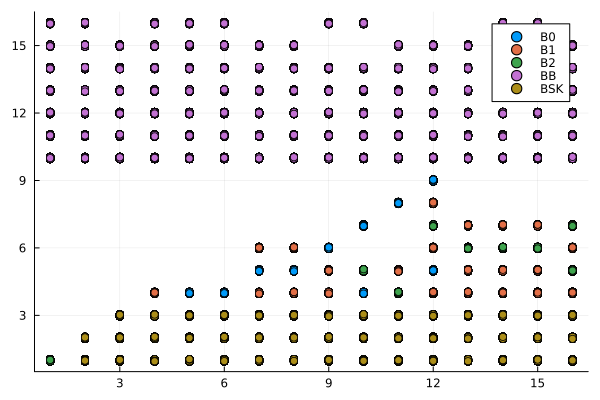
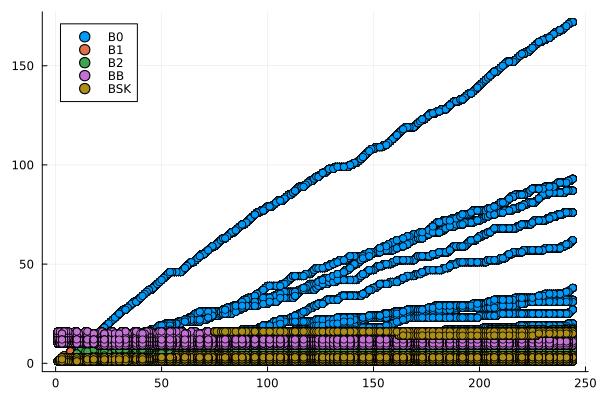
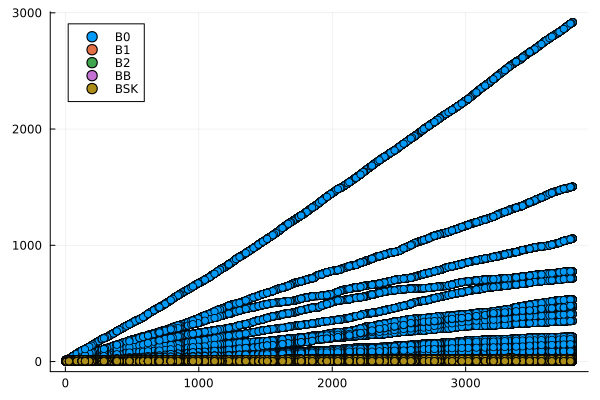
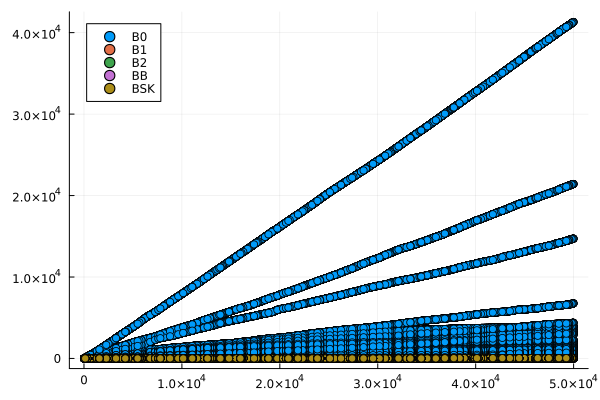
Se esperaba que los algoritmos implementados tuvieran un desempeño proporcional al logaritmo del valor buscado, por lo que tenían un desempeño óptimo. Sin embargo, los resultados obtenidos arrojaron un desempeño con una tendencia no discernible con respecto al valor buscado y orden de los ejes inesperado: en el caso de los tiempos de ejecución, el eje es igual para cada consulta, mientras qque en el de la contabilidad de operaciones, este tiene la misma escala que el eje horizontal. Esta situación es diferente a la esperada y puede obedecer a errores en la implementación de los algoritmos o a un rendimiento inesperado de estos. Es necesario una mayor profundización en el estudio de los algoritmos para determinar la causa de este comportamiento.

5 Referencia

Téllez Avila, Eric Sadit. 2025. Curso Introductorio al Análisis de Algoritmos con Julia. https://sadit.github.io/ALGO-IR/.

Notas

Datos originalmente disponibles Téllez Avila (2025). Revise la licencia en dicha página y consulte el aviso legal.↩︎

--- title: 'Algoritmos de búsqueda por comparación' date: 2025-04-01 jupyter: julia-1.11 description: 'Análisis de algoritmos de búsqueda adaptativa en Julia, comparando eficiencia entre métodos binarios, secuenciales y SkipLists.' categories: - Análisis de algoritmos - Julia - Algoritmos de búsqueda - Búsqueda binaria - Búsqueda acotada image: portada_busqueda_comparacion.png --- ![](portada_busqueda_comparacion.png) ```{julia} #| label: software using Dates, DataFrames, JSON, MarkdownTables, Random, StatsPlots rng = Xoshiro(20250331) ``` # Introducción @sadit_algoritmos[capítulo 5] discute algoritmos adaptables de búsqueda en arreglos organizados. En el modelo de comparación, estos algoritmos buscan identificar la posición de inserción, $p$, en la que debe acomodarse un valor $x$ para que el arreglo $A = (a_1, \dots, a_n), \, a_1 \leq \dots \leq a_n$ se mantenga ordenado después de la inserción de $x$. En la @sec-busqueda se presentan e implementan en `Julia` los algoritmos analizados, tanto para el caso base (la búsqueda binaria), cuyo costo depende del tamaño del arreglo, como para los algoritmos adaptables. Como se observa en dicha sección, la particularidad de estos últimos es que su costo de ejecución depende de $p$ y no del tamaño del arreglo. A continuación, en la @sec-experimentos se implementan diversos experimentos para probar cada algoritmo en cuanto al tiempo de ejecución y el número de operaciones de comparación requeridas. Al respecto, se observa que en los experimentos realizados no se observa una tendencia clara en los datos que permita identificar si se satisface la expectativa de que el tiempo de ejecución y el número de operaciones de los algoritmos analizados dependen de $p$. Por lo tanto, en la @sec-conclusion se concluye que se requiere mayor investigación para determinar la causa del comportamiento inesperado. # Algoritmos de búsqueda {#sec-busqueda} En esta sección se analizan diversos algoritmos de búsqueda descritos en @sadit_algoritmos[capítulo 5], así como una implementación propia de un algoritmo de búsqueda sobre SkipLists. Para cada uno, se explica cuál es el costo del problema y se describe una función en `Julia` para su implementación. ## Búsqueda binaria acotada {#sec-binaria} La búsqueda binaria en el subarreglo $A[i:f]$ consiste en verificar si $x$ se encuentra antes o después del punto medio, $m = \lfloor \frac{i + f}{2} \rfloor$, para lo cual se debe comparar $x$ con $a_m$, actualizar $i$ o $f$ para continuar la búsqueda en un arreglo de la mitad del tamaño e iterar hasta llegar al caso base, en donde $i \geq f$. Cuando se llega a ese punto, entonces únicamente hay que comparar $x$ con el valor de $a_i$ correspondiente y seleccionar $p$ como $i$ o $i + 1$, dependiendo del resultado obtenido. Esta implementación obtiene un costo de búsqueda de $O(\log_2 n)$ [@sadit_algoritmos, sección 5.1.1]. Este algoritmo fue implementado en `Julia` mediante la función `busqueda_binaria()`, en la que se adicionó un argumento opcional para contabilizar el número de veces que se calcula el punto medio, que corresponde al costo del problema. ```{julia} #| label: funcion_busqueda_binaria function busqueda_binaria( A::Vector{T}, x::T, c::Union{Nothing, Int64} = nothing, inicio::Int64 = 1, final::Int64 = length(A) ) where {T} while inicio < final medio = (inicio + final) ÷ 2 if x <= A[medio] final = medio else inicio = medio + 1 end if c isa Int64 c += 1 end end p = x <= A[inicio] ? inicio : inicio + 1 return p, c end ``` ```{julia} #| label: verificar_busqueda_binaria #| include: false # Funciona bien :) for x in [0, 69, 70, 71] println( busqueda_binaria([10, 20, 30, 40, 50, 60, 70], x) ) println( busqueda_binaria([10, 20, 30, 40, 50, 60, 70], x, 0) ) end ``` De acuerdo con @sadit_algoritmos[sección 5.2], cuando $n \to \infty$ o la relación $\frac{p}{n} \to 0$, es más útil definir un rango que pueda contener la respuesta antes de aplicar la búsqueda binaria. Esto se puede implementar mediante una familia de algoritmos $B_k$, cuyos primeros miembros se explican e implementan en las siguientes subsecciones. También se explica un algoritmo basado en la estructura SkipLists que tiene esta misma inspiración. Con base en esta observación, el único algoritmo de búsqueda que depende del tamaño del arreglo, $n$, que se analiza en este documento es el implementado mediante `busqueda_binaria()`. En las siguientes subsecciones, se presentan algoritmos adaptativos que dependen de $p$. ## Búsqueda secuencial $B_0$ Sea $F_0(n) = 1, 2, \dots, n, n + 1$ una secuencia de puntos en los que se harán comparaciones entre $x$ y $a_{F_0(n)}$. Es decir, este algoritmo implementa una búsqueda exhaustiva al comparar $x$ con cada valor del arreglo $A$, por lo que no requiere una búsqueda binaria y su costo de búsqueda corresponde a todas las comparaciones que se deben hacer hasta llegar a la posición de inserción $C_0(p) = p + 1$ [@sadit_algoritmos, sección 5.2.1]. Para implementar el algoritmo, se debe iniciar la búsqueda en el primer elemento de A y continuarla hasta que se encuentre el elemento de $A$ que sea mayor que $x$ o se recorra todo el arreglo, entonces la posición de inserción de $x$ será la posición de dicho elemento [@sadit_algoritmos, sección 5.1.1]. Este algoritmo se implementó en `Julia` mediante la función `busqueda_b0()`, en la que se adicionó un argumento opcional para contabilizar el número de veces que se realizan comparaciones, que corresponde al costo del problema. ```{julia} #| label: funcion_busqueda_b0 function busqueda_b0( A1::Vector{T}, x::T, c::Union{Nothing, Int64} = nothing, inicio::Int64 = 1) where {T} p = 1 A = A1[inicio:end] n = length(A) while p <= n && x > A[p] p += 1 if c isa Int64 c += 1 end end return p, c end ``` ```{julia} #| label: verificar_busqueda_b0 #| include: false # Funciona bien :) # Preguntar si el costo es p - 1 for x in [0, 69, 70, 71] println( busqueda_b0([10, 20, 30, 40, 50, 60, 70], x) ) println( busqueda_b0([10, 20, 30, 40, 50, 60, 70], x, 0) ) end ``` ## Búsqueda secuencial $B_1$ Sea $F_1(n) = 2^1, 2^2, \dots, 2^{\lfloor \log_2 n \rfloor + 1}$ una secuencia de puntos en los que se harán comparaciones entre $x$ y $a_{F_1(n)}$, que servirán para determinar el rango en el que se realizará la búsqueda binaria $A[2^{\lfloor \log_2 p \rfloor + 1}:2^{\lfloor \log_2 (p + 1) \rfloor + 1}]$; entonces, dependiendo de la posición $p$, el número de comparaciones que se deben realizar para determinar este rango está determinado por $\lfloor \log_2 p + 1 \rfloor + 1$. Una vez determinado, el costo de la búsqueda en dicho rango está limitado por $O(\log_2 n^\prime)$ donde $n^\prime$ es el tamaño del arreglo en el que se realiza la búsqueda binaria. Por lo tanto, el costo total de la búsqueda implementada es $C_1(p) < 2 \log_2 p + O(1)$ [@sadit_algoritmos, sección 5.2.2]. Este algoritmo se implementó en `Julia` mediante la función `busqueda_b1()`, en la que se adicionó un argumento opcional para contabilizar el número de veces que se realizan comparaciones, que corresponde al costo del problema. ```{julia} #| label: funcion_busqueda_b1 function busqueda_b1( A1::Vector{T}, x::T, c::Union{Nothing, Int64} = nothing, inicio::Int64 = 1) where {T} A = A1[inicio:end] n = length(A) p = 0 # Determinar el rango # Duplicar la posición de búsqueda e ir actualizando la posición de inicio iteracion = 1 while iteracion + 1 <= n && A[iteracion + 1] < x p = iteracion iteracion *= 2 if c isa Int64 c += 1 end end # Realizar la búsqueda dentro del rango p, c = busqueda_binaria(A, x, c, p + 1, min(n, iteracion + 1)) return p, c end ``` ```{julia} #| label: verificar_busqueda_b1 #| include: false # Funciona bien :) for x in [0, 69, 70, 71] println( busqueda_b1([10, 20, 30, 40, 50, 60, 70], x) ) println( busqueda_b1([10, 20, 30, 40, 50, 60, 70], x, 0) ) end ``` ## Búsqueda secuencial $B_2$ Sea $F_2(n) = 2^{2^1}, 2^{2^2}, \dots, 2^{2^{\lfloor \log_2 \lfloor \log_2 (p + 1) + 1 \rfloor + 1}}$ una secuencia de puntos en los que se harán comparaciones entre $x$ y $a_{F_2(n)}$, que servirán para determinar el rango en el que se realizará la búsqueda de información $A[2^{2 \lfloor \log_2 \lfloor \log_2 p \rfloor + 1 \rfloor + 1}:2^{2 \lfloor \log_2 \lfloor \log_2 (p + 1) \rfloor + 1 \rfloor + 1}]$; entonces, dependiendo de la posición $p$, el número de comparaciones que se deben realizar para determinar este rango está determinado por $\lfloor \log_2 \lfloor \log_2 (p + 1) \rfloor + 1 \rfloor + 1$. Una vez determinado este rango, se puede aplicar la búsqueda $B_1$ sobre él. Por lo tanto, el costo total de la búsqueda implementada es $C_2(p) < \log_2 p + 2 \log_2 \log_2 p + O(1)$ [@sadit_algoritmos, sección 5.2.2]. Este algoritmo se implementó en `Julia` mediante la función `busqueda_b2()`, en la que se adicionó un argumento opcional para contabilizar el número de veces que se realizan comparaciones, que corresponde al costo del problema. ```{julia} #| label: funcion_busqueda_b2 function busqueda_b2( A1::Vector{T}, x::T, c::Union{Nothing, Int64} = nothing, inicio::Int64 = 1 ) where {T} A = A1[inicio:end] n = length(A) p1 = 0 # Determinar el rango # Duplicar la posición de búsqueda e ir actualizando la posición de inicio iteracion = 1 valor = 2^(2^iteracion) while valor + 1 <= n && A[valor + 1] < x p1 = valor iteracion += 1 valor = 2^(2^iteracion) if c isa Int64 c += 1 end end # Realizar la búsqueda dentro del rango p, c = busqueda_b1(A[(p1 + 1):min(valor, n)], x, c) return p + p1, c end ``` ```{julia} #| label: verificar_funcion_busqueda_b2 #| include: false # Funciona bien :) for x in [0, 69, 70, 71] println( busqueda_b2([10, 20, 30, 40, 50, 60, 70], x) ) println( busqueda_b2([10, 20, 30, 40, 50, 60, 70], x, 0) ) end ``` ## Busqueda mediante SkipLists Como se explicó en [el post sobre algoritmos de ordenamiento](../20250304-algoritmos_ordenamiento/index.qmd), se puede implementar una "*SkipList*" en `Julia` mediante las estructuras mutables `Nodo` y `Lista_Salto`, como se muestra a continuación. A partir de estas estructuras, se pueden definir funciones para modificar la lista al insertar elementos en ella, `inserta_skiplist!()`, y utilizar el resultado obtenido para ordenar un arreglo, `ordenar_skiplist()`. ```{julia} #| label: estructuras_skiplist #| code-fold: show # 1. Estructuras de datos # Nodos mutable struct Nodo{T} valor::T sucesores::Vector{ Union{Nodo{T}, Nothing} } end Nodo{T}(valor::T, nivel::Int64) where {T} = Nodo{T}( valor, Vector{ Union{Nodo{T}, Nothing} }(nothing, nivel) ) Nodo(valor::T, nivel::Int64) where {T} = Nodo{T}(valor::T, nivel::Int64) # Listas mutable struct Lista_Salto{T} nivel_maximo::Int64 cabeceras::Vector{ Union{Nodo{T}, Nothing} } end Lista_Salto{T}() where {T} = Lista_Salto( 1, Vector{ Union{Nodo{T}, Nothing}}(nothing, 1) ) Lista_Salto() = Lista_Salto{Float64}() # 2. Función inserta_skiplist!() function inserta_skiplist!( lista::Lista_Salto{T}, valor::T, c::Union{ Int64, Nothing } = nothing, rng = nothing) where {T} # Asignar aleatoriamente un nivel nivel = 1 if rng isa Nothing while rand() <= 0.5 nivel += 1 end else while rand(rng) <= 0.5 nivel += 1 end end # Si la lista tiene menos niveles, adicionar los restantes if nivel > lista.nivel_maximo for k in (lista.nivel_maximo + 1):nivel push!(lista.cabeceras, nothing) end lista.nivel_maximo = nivel end # Nuevo nodo y = Nodo{T}(valor, nivel) # Actualizar los punteros desde el máximo nivel que estoy insertando for k in nivel:-1:1 # Contabilizar el número de actualizaciones del puntero if c isa Int64 c += 1 end x = lista.cabeceras[k] if x isa Nothing # Si el nivel k de la cabecera está vacío, entonces apunta # al nuevo nodo lista.cabeceras[k] = y elseif valor < x.valor # Si lo que se inserta es pequeño, entonces se actualiza desde # el principio lista.cabeceras[k] = y y.sucesores[k] = x else # Si no está vacío, buscamos hasta que el nivel de algún # sucesor sea menor y quebramos los apuntadores z = x.sucesores[k] while !(z isa Nothing) && (valor > z.valor) x = z z = z.sucesores[k] end x.sucesores[k] = y y.sucesores[k] = z end end return c end # 3. Función ordenar_skiplist() function ordenar_skiplist( a::Vector, c::Union{ Int64, Nothing } = nothing, rng = nothing) listado = Lista_Salto{eltype(a)}() ordenar = Vector{eltype(a)}() for elemento in a c = inserta_skiplist!(listado, elemento, c, rng) end siguiente = listado.cabeceras[1] while !(siguiente isa Nothing) push!(ordenar, siguiente.valor) siguiente = siguiente.sucesores[1] end return c, ordenar, listado end ``` En adición a los elementos señalados, que ya habían sido analizados en ese post, se generó la función `busqueda_skiplist()`, que implementa un algoritmo adaptativo para buscar un valor $x$ en una SkipList. A diferencia de los algoritmos señalados en las subsecciones anteriores, este no entrega la posición en la cual se debe insertar el valor para conservar el orden del arreglo, pues ello no tiene sentido para una SkipList, sino que entrega la referencia del nodo que sería antecesor al que se construya a partir del valor que se desea insertar, de forma que los apuntadores después de insertar el nodo con este valor mantengan el ordenamiento de la lista. El procedimiento implementado se describe a continuación: + Se busca el valor al que apuntan las cabeceras de la lista en las posiciones $F(n) = 2^0, 2^1, \dots, 2^{\lfloor \log_2 n + 1 \rfloor}$. + Se identifica el nodo con el valor más grande en dicha lista, cuyo valor es inferior al valor buscado $x$. Es decir, se reduce la dimensionalidad del rango buscado al eliminar los primeros nodos más pequeños que el valor buscado. + Se realiza una búsqueda descendiendo de nivel, del nodo más grande en la lista que es inferior al valor buscado. Se adicionó un parámetro opcional en esta función que contabiliza el número de comparaciones que realiza el algoritmo, que es proporcional a su costo de ejecución. Debido al primer inciso señalado, se espera que este costo sea proporcional al valor de $p$, no al tamaño completo de la SkipList. ```{julia} #| label: funcion_busqueda_skiplist function busqueda_skiplist( lista::Lista_Salto{T}, valor::T, c::Union{ Int64, Nothing } = nothing ) where {T} k = 1 while k <= lista.nivel_maximo && lista.cabeceras[k].valor < valor k *= 2 if c isa Int64 c += 1 end end k = min(k, lista.nivel_maximo) if lista.cabeceras[k].valor >= valor inferior = lista.cabeceras else inferior = lista.cabeceras[k] while k >= 1 # Contabilizar el número de actualizaciones del puntero if c isa Int64 c += 1 end siguiente = inferior.sucesores[k] if siguiente isa Nothing || siguiente.valor >= valor k -= 1 else # Si no está vacío, buscamos hasta que el nivel de algún # sucesor sea menor y quebramos los apuntadores inferior = siguiente end end end return inferior, c end ``` ```{julia} #| label: verificar_busqueda_skiplist #| include: false # Funciona bien :) _, _, lista = ordenar_skiplist([10, 20, 30, 40, 50, 60, 70], nothing, rng) for x in [0, 69, 70, 71] println( busqueda_skiplist( lista, x ) ) println( busqueda_skiplist( lista, x, 0) ) end ``` # Experimentos {#sec-experimentos} Como fue señalado en la sección anterior, se espera que el costo de ejecución de `busqueda_binaria()` sea proporcional al tamaño del arreglo, mientras que el de las demás funciones debería ser proporcional a $p$. En este sentido, en esta sección se realizan experimentos con diversos valores de $p$ para verificar si se satisface esta expectativa teórica en las funciones implementadas. En la @sec-datos se describen los datos utilizados y las consultas que fueron realizadas sobre ellos. En la @sec-tiempo, se analizan los tiempos de ejecución y en la @sec-cuenta se contabiliza el número de operaciones. En ambos casos, se observa que se los resultados obtenidos no fueron los esperados. ## Datos {#sec-datos} Se generó el mismo diccionario denominado `datos` disponible en el [el post sobre algoritmos de ordenamiento](../20250304-algoritmos_ordenamiento/index.qmd). ```{julia} #| label: importa_datos #| eval: false datos = Dict() for numero in ["016", "032", "064", "128", "256", "512"] datos[parse(Int64, numero)] = JSON.parsefile( "../20250304-algoritmos_ordenamiento/listas-posteo-con-perturbaciones-p=$(numero).json" ) end for numero in keys(datos) for asunto in keys(datos[numero]) datos[numero][asunto] = convert(Vector{Int64}, datos[numero][asunto]) end datos[numero] = convert(Dict{String, Vector{Int64}}, datos[numero]) end datos = convert(Dict{Int64, Dict{String, Vector{Int64}}}, datos) ``` Como las funciones `busqueda_binaria()`, `busqueda_b0()`, `busqueda_b1()` y `busqueda_b2()` requieren como entrada un arreglo ordenado y la función `busqueda_skiplist()` requiere una SkipList, entonces se procesaron los arreglos desordenados originalmente disponibles en cada diccionario interior para convertirlos en uno de estos dos tipos de insumo. Para ello, cada uno de los arreglos originales se procesó mediante la función `ordenar_skiplist()` y se conservaron las respuestas del arreglo ordenado y la SkipList que se obtienen a partir de esta función; estos arreglos se registraron en los diccionarios denominados `ordenado` y `skiplist`, respectivamente. ```{julia} #| label: arreglos_ordenados #| eval: false ordenado = Dict{Int64, Dict{String, Vector{Int64}}}() skiplist = Dict{Int64, Dict{String, Lista_Salto{Int64}}}() for numero in keys(datos) ordenado[numero] = Dict{String, Vector{Int64}}() skiplist[numero] = Dict{String, Lista_Salto{Int64}}() for asunto in keys(datos[numero]) _, x, y = ordenar_skiplist( datos[numero][asunto] ) ordenado[numero][asunto] = x skiplist[numero][asunto] = y end end ``` Asimismo, se obtuvieron números para consultar en los diferentes arreglos a partir de 4 archivos electrónicos, [disponibles aquí](https://www.dropbox.com/scl/fo/8zrqyv1603qfxj2a3w29b/ALkCU_d2_-Ui5zVZ5BBd1DE?rlkey=mwkqer63q8uyzivplmg4ygwuh&st=wr2ej92s&dl=0).^[Datos originalmente disponibles [@sadit_algoritmos](https://github.com/sadit/ALGO-IR/). Revise la licencia en dicha página y consulte el [aviso legal](../../legal.qmd).] Estos se registraron en un diccionario denominado `consultas`, cuyas claves son asociadas al archivo electrónico correspondiente y cuyos valores son los arreglos con los números de consulta que se realizarán. ```{julia} #| label: consultas #| eval: false consultas = Dict() for numero in [1, 2, 3, 4] consultas[numero] = JSON.parsefile("consultas-$(numero)-listas-posteo.json") end for numero in keys(consultas) consultas[numero] = convert(Vector{Int64}, consultas[numero]) end consultas = convert(Dict{Int64, Vector{Int64}}, consultas) ``` ## Tiempo de ejecución {#sec-tiempo} Se observó que cada una de las claves en `ordenado` contienen vectores con la misma información. Por lo tanto, únicamente se realizarán consultas sobre los vectores disponibles en `ordenado[16]` y `skiplist[16]`, en lugar de hacerlo para cada clave en dichos diccionarios. Para cada una de las consultas disponibles en los elementos de `consultas`, se iteró 100 veces sobre los arreglos señalados y se midió el tiempo total de ejecución de las funciones disponibles en la @sec-busqueda. Cada una de las observaciones se registró en un `DataFrame` denominado `labbusc`, que contiene los siguientes campos: + `funcion`, que contiene una abreviatura asociada a la función de búsqueda utilizada. + `num_consulta`, que corresponde al número del archivo de consulta utilizado. + `consulta`, que corresponde al valor buscado en los vectores de `ordenado[16]` y `skiplist[16]`. + `tiempo`, que corresponde al tiempo total utilizado para realizar las 100 iteraciones de la consulta ```{julia} #| label: labbusc_tiempo #| eval: false experimentos = [ ("busqueda_binaria", "BB"), ("busqueda_b0", "B0"), ("busqueda_b1", "B1"), ("busqueda_b2", "B2"), ("busqueda_skiplist", "BSK")] labbusc_tiempo = DataFrame( funcion = Vector{String}(), num_consulta = Vector{Int64}(), consulta = Vector{Int64}(), tiempo = Vector{Float64}() ) n_iter = 100 # Vamos a guardar el número de la consulta, el experimento y cuánto se demora realizándola, # independientemente de la lista de posteo (ya da igual porque están organizados) for num_consulta in 1:4 for consulta in consultas[num_consulta] for experimento in experimentos # Midamos el tiempo que se demora cada función en buscar cada # consulta en todos los vectores de las listas de posteo f = Symbol(experimento[1]) f = getfield(Main, f) x = now() for asunto in keys(ordenado[16]) for i in 1:n_iter if experimento[1] != "busqueda_skiplist" f(ordenado[16][asunto], consulta) else f(skiplist[16][asunto], consulta) end end push!(labbusc_tiempo, (experimento[2], num_consulta, consulta, Dates.value( Millisecond(now() - x) ) ) ) end end end end ``` Con base en esta información se generaron gráficos de dispersión, para cada archivo de consultas, que muestran el logaritmo en base 10 del tiempo que toma cada función para ejecutar las consultas en los vectores ordenados como función del valor consultado $p$. Estas se muestran en la @fig-labbusc_tiempo. ```{julia} #| label: grafico-busquedas_tiempo #| eval: false jitter(n::Real, factor = 0.1) = n + (0.5 - rand()) * factor labbusc_tiempo = filter(row -> !isnan(row.tiempo) && row.tiempo > 0, labbusc_tiempo) for i in 1:4 grafico = filter(row -> row.num_consulta == i, labbusc_tiempo) plot = @df grafico scatter(:consulta, jitter.(log10.(:tiempo)), group = :funcion) savefig(plot, "busquedas_$(i)_tiempo.png") end ``` ::: {#fig-labbusc_tiempo layout-ncol=2} ![Consultas 1](busquedas_1_tiempo.png) ![Consultas 2](busquedas_2_tiempo.png) ![Consultas 3](busquedas_3_tiempo.png) ![Consultas 4](busquedas_4_tiempo.png) Tiempos de ejecución ::: ## Contabilización del número de comparaciones {#sec-cuenta} Homólogamente, se contabilizó el número de comparaciones que requirió cada algoritmo para realizar la búsqueda de cada valor. A diferencia del caso anterior, este experimento se realizó una única vez por experimento, pues el número de comparaciones es determinístico. ```{julia} #| label: labbusc_cuenta #| eval: false labbusc_cuenta = DataFrame( funcion = Vector{String}(), num_consulta = Vector{Int64}(), consulta = Vector{Int64}(), contabilidad = Vector{Float64}() ) # Vamos a guardar el número de la consulta, el experimento y cuántas comparaciones hace, # independientemente de la lista de posteo (ya da igual porque están organizados) for num_consulta in 1:4 for consulta in consultas[num_consulta] for experimento in experimentos # Midamos el tiempo que se demora cada función en buscar cada # consulta en todos los vectores de las listas de posteo f = Symbol(experimento[1]) f = getfield(Main, f) x = now() for asunto in keys(ordenado[16]) if experimento[1] != "busqueda_skiplist" _, c = f(ordenado[16][asunto], consulta, 0) else _, c = f(skiplist[16][asunto], consulta, 0) end push!(labbusc_cuenta, (experimento[2], num_consulta, consulta, c) ) end end end end ``` Con base en esta información se generaron gráficos de dispersión, para cada archivo de consultas, que muestran el número de comparaciones que requiere cada función para ejecutar las consultas en los vectores ordenados, como función del valor consultado $p$. Estas se muestran en la @fig-labbusc_cuenta. ```{julia} #| label: grafico-busquedas_cuenta #| eval: false labbusc_cuenta = filter(row -> !isnan(row.contabilidad) && row.contabilidad > 0, labbusc_cuenta) for i in 1:4 grafico = filter(row -> row.num_consulta == i, labbusc_cuenta) plot = @df grafico scatter(:consulta, jitter.(:contabilidad), group = :funcion) savefig(plot, "busquedas_$(i)_cuenta.png") end ``` ::: {#fig-labbusc_cuenta layout-ncol=2} ![Consultas 1](busquedas_1_cuenta.png) ![Consultas 2](busquedas_2_cuenta.png) ![Consultas 3](busquedas_3_cuenta.png) ![Consultas 4](busquedas_4_cuenta.png) Cantidad de operaciones ::: # Conclusión {#sec-conclusion} Se esperaba que los algoritmos implementados tuvieran un desempeño proporcional al logaritmo del valor buscado, por lo que tenían un desempeño óptimo. Sin embargo, los resultados obtenidos arrojaron un desempeño con una tendencia no discernible con respecto al valor buscado y orden de los ejes inesperado: en el caso de los tiempos de ejecución, el eje es igual para cada consulta, mientras qque en el de la contabilidad de operaciones, este tiene la misma escala que el eje horizontal. Esta situación es diferente a la esperada y puede obedecer a errores en la implementación de los algoritmos o a un rendimiento inesperado de estos. Es necesario una mayor profundización en el estudio de los algoritmos para determinar la causa de este comportamiento. # Referencia

Algoritmos de búsqueda por comparación

1 Introducción

2 Algoritmos de búsqueda

2.1 Búsqueda binaria acotada

2.2 Búsqueda secuencial \(B_0\)

2.3 Búsqueda secuencial \(B_1\)

2.4 Búsqueda secuencial \(B_2\)

2.5 Busqueda mediante SkipLists

3 Experimentos

3.1 Datos

3.2 Tiempo de ejecución

3.3 Contabilización del número de comparaciones

4 Conclusión

5 Referencia

Notas